Question

For each question below, use the function f (x) = x3

A. On what interval(s) is this function negative?
B. What is/are the roots of this function?
C. What is the end behavior of this function?

Answer 1

A. The function is negative on the interval (-∞, 0)

B. The only root is x = 0

C. The function approaches ∞ when x gets really large (goes towards ∞). The function approaches -∞ when x gets really small (goes towards -∞).

Explanation:

The function given is
`f(x)=x^3`

The graph is attached. Looking at the graph will make understanding the solutions easier.

A.

We need to find the intervals that is divided by the roots of the function.

To find x-intercepts, we set
`f(x)=0`

`f(x)=x^3\\0=x^3\\x=0`

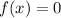
*Looking at the graph, we can also see that x=0 is the only x-intercept*

Thus the intervals are from -∞ to 0 and from 0 to ∞

We take value in each interval to determine whether the function is negative or positive. If the answer is positive, function is increasing, if negative, the function is decreasing.

• From -∞ to 0, we take x = -1

`f(-1)=(-1)^3\\=-1`

Hence it is decreasing

• From 0 to ∞, we take x = 1

`f(1)=(1)^3\\=1`

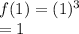
Hence it is increasing

The function is negative on the interval (-∞, 0)

B.

To find the roots, x-intercepts, we set
`f(x)=0`

`f(x)=x^3\\0=x^3\\x=0`

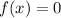
The only root is x = 0

C.

To find end behavior, we look at the graph.

The end behavior means what happens to the function when x goes to ∞ and -∞

Looking at the graph, the function approaches ∞ when x gets really large (goes towards ∞). The function approaches -∞ when x gets really small (goes towards -∞).

*Also, if you plug in large x values, f(x) goes towards infinity. If you plug in small x values, f(x) goes towards negative infinity*

Answer 2

A. (-∞ , 0)

B. x = 0 triple root

C. The function tends to infinity

Explanation:

For the function f(x) = x^3 we have:

Negative intervals:

(-∞ , 0)

The roots of this function is:

x = 0

The final behavior of this function tends toward infinity

A graphic is attached below