Question

Given: Triangle ADE~

Triangle CBF, ED bisects Angle ADC and F B bisects Angle ABC.
Prove: DF BE is a parallelogram.

Answer 1

See proof below

Explanation:

Given
`\triangle ADE \cong \triangle CBD`

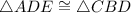
Then,
`\angle AED \cong \angle CFB` because corresponding parts of congruent triangles are congruent.

Since
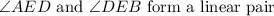`\angle AED \text{ and } \angle DEB \text{ form a linear pair}`, by the linear pair postulate,
`\angle AED \text{ and } \angle DEB \text{ are supplementary}`.

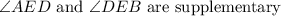Similarly,
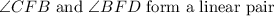`\angle CFB \text{ and } \angle BFD \text{ form a linear pair}`, so by the linear pair postulate,
`\angle CFB \text{ and } \angle BFD \text{ are supplementary}`.

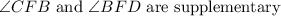By the Congruent supplements theorem, since
`\angle AED \text{ and } \angle DEB \text{ are supplementary}`,
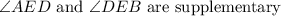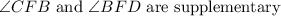`\angle CFB \text{ and } \angle BFD \text{ are supplementary}`, and
`\angle AED \cong \angle CFB` , then
`\angle DEB \cong \angle BFD`. (note, this is one pair of opposite angles inside quadrilateral DFBE)

Recalling that
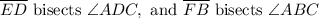`\overline {ED} \text{ bisects } \angle ADC, \text{ and } \overline {FB} \text{ bisects } \angle ABC`, then,
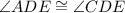`\angle ADE \cong \angle CDE`, and
`\angle CBF \cong \angle FBA` by definition of angle bisector.

Note that
`\angle ADE \cong \angle CBF` because corresponding parts of congruent triangles are congruent.

Also, note that
`\angle EDF \cong \angle EDC` and
`\angle FBA \cong \angle FBE` because B, E, A are colinear, and D, F, C are colinear.

So, by the transitive property of angle congruence,
`\angle EDF \cong \angle FBE` (This is the other pair of opposite angles inside quadrilateral DFBE)

So, since both pairs of opposite angles are congruent, quadrilateral DFBE is a parallelogram, by a theorem about quadrilateral properties (your book may or may not have a name for it. It may just have a number).