Answer:
V₂ = 7.43 m/s
Step-by-step explanation:
To find the velocity of the second ball after the collision, we will use the following formula:
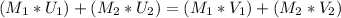
where M₁ = mass of ball 1 = 4.6 kg
M₂ = mass of ball 2 = 4.6 kg
U₁ = velocity of ball 1 before collision = 7.43 m/s
U₂ = velocity of ball 2 before collision = 0 m/s
V₁ = velocity of ball 1 after collision = 0 m/s
V₂ = velocity of ball 1 after collision = ?
So substituting the given values in the above formula to get:
(4.6 × 7.43) + (4.6 × 0) = (4.6 × 0) + (4.6 × V₂)
34.178 = (4.6)V₂
V₂ = 7.43 m/s