Question

△XYZ maps to △MNO with the transformation (x, y) ---> (5x, 5y).

If XY = 6, what is the length of MN?

Answer 1

The length of MN is 30.

Explanation:

It is given that △XYZ maps to △MNO with the transformation

`(x,y)\rightarrow (5x,5y)`

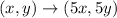
This rule of transformation represents the dilation with scale factor 5 because the dilation about the origin is defined as

`(x,y)\rightarrow (kx,ky)`

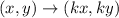
where, k is scale factor.

In dilation, the image and preimage are similar and scale factor is the ratio of corresponding side of image and preimage.

In △XYZ and △MNO,

`k=(MN)/(XY)`

`5=(MN)/(6)`

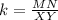
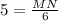
Multiply both sides by 6.

`30=MN`

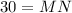
Therefore the length of MN is 30.