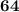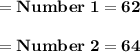SOLVING
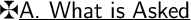
Find two consecutive even numbers whose sum is 126.

For now, let the first number be x.
Let the second number be x+2. (consecutive even numbers are right next to each other, like 2 and 4)
These two integers add up to 126. This gives us an equation that we can solve in terms of x.
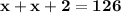 | arrange the like terms
| arrange the like terms
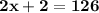 | subtract 2
| subtract 2
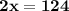 | 2 was subtracted from BOTH sides
| 2 was subtracted from BOTH sides


Now, the second integer is
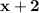 .
.
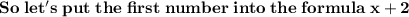 .
.
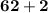 | add (mental arithmetic)
| add (mental arithmetic)