Question

What is the solution of the system of equations? {4x−3y=152x+2y=4 Enter your answer in the boxes.

Answer 1

3, -1

I just took the test so enjoy

Answer 2

x = 3, y = -1

Explanation:

`\left \{ {{4x-3y=15} \atop {2x+2y=4}} \right.`

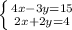
To solve this, we will eliminate x. In order to do this, we must multiply the bottom equation by 2:

`\left \{ {{4x-3y=15} \atop {2(2x+2y=4)}} \right. \\\\\left \{ {{4x-3y=15} \atop {4x+4y=8}} \right.`

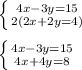
To eliminate x, we will subtract the bottom equation from the top one:

`\left \{ {{4x-3y=15} \atop {-(4x+4y=8)}} \right. \\\\-3y-4y=15-8\\\\-7y=7`

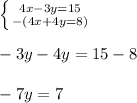
Divide both sides by -7:

-7y/-7 = 7/-7

y = -1

Substitute this into the first equation:

4x-3(-1) = 15

4x--3 = 15

4x+3 = 15

Subtract 3 from each side:

4x+3-3 = 15-3

4x = 12

Divide both sides by 4:

4x/4 = 12/4

x = 3