Take the first derivative to find critical points:

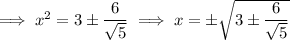
or approximately (from least to greatest) -2.4, -0.56, 0.56, 2.4.
We have second derivative
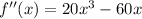
and at each of the critical points, we have
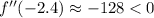
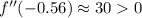
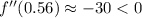
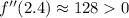
The signs of the second derivative at each point indicates a local minima at
 and
and
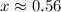 , and local maxima at
, and local maxima at
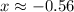 and
and
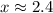 . At these extrema, we have
. At these extrema, we have
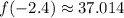
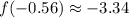

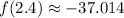
and at the endpoints of the interval, we have

So the answer is A.