Question

Complete the square to solve 2x^2+20x=10

Answer 1

The Solution of the equation is

x= 5 ±
`2√(5)`

Explanation:

We are supposed to find the solution of the equation by completing square method

our given equation is

2x² + 20x + 10 = 0

Dividing whole equation by 2

we will get

x² + 10 x + 5 = 0

Now we will write the middle term in factor form to see what we will be needing to make it perfect square

it would be written as

x² + 2(5) x + 5 = 0

Now adding 20 on both sides we get

x² + 2(5) x + 5 + 20 = 20

x² + 2(5) x + 25 = 20

(x)² + 2(5) x +(5)² = 20

Now we have the form of a²+2(a)(b) + b²

And also we know that

a²+2(a)(b) + b² = (a+b)²

So our equation becomes

(x+5)² = 20

Taking square root of both sides it becomes

`\sqrt{(x+5)^(2) }=√(20)`

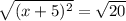
square cuts out with square root so

it becomes

x+5 = ±
`√(20)`

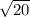
We know that
`√(20)=2√(5)`

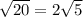
So it becomes

x+5 =±
`2√(5)`

Subtracting 5 from both sides

it becomes

x= 5 ±
`2√(5)`

So

The Solution of the equation is

x= 5 ±
`2√(5)`

Answer 2

x = (-5 + √30) and x = (-5 - √30)

Explanation:

The given expression is 2x² + 20x = 10

To find the solution of x we will convert this expression into a perfect square.

2(x² + 10x) = 10

x² + 10x = 5

x² + 10x + 25 = 5 + 25

(x + 5)² = 30 [ since (a + b)² = a² + b² + 2ab ]

x + 5 = ±√30

x = (- 5 ± √30)

Therefore solutions are x = (-5 + √30) and x = (-5 - √30)