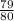Answer: The probability of Beth getting selected is
Explanation:
Since we have given that
Probability of selecting Jim is given by
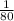
According to question, Jim and Beth are both member of a population.
As we know that ,

So, using this , we get chances of Beth being selected:
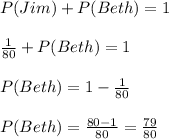
Hence, the probability of Beth getting selected is