Question

Based on the shortest leg of the triangle illustrated, if a similar triangle on the coordinate plane has its shortest leg defined by the points (-2, 4) and (-6, 0), what is the third point?

Answer 1

(-2, -8)

Explanation:

The similarity ratio is 2.

All corresponding sides of similar triangles are proportional.

Answer 2

In a triangle ,shortest leg is located in the coordinate plane at B (-2,4) and C(-6,0).

Distance between two points in two dimensional plane is given by =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2`

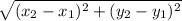
BC=
`√((-2 +6)^2+(4-0)^2)=√(16+16)=√(32)=4√(2)`

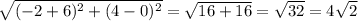
= 4 × 1.414

= 5.656

Let A (p,q), be the Third vertex of ΔA BC.There will be no single point. We can find the locus of point A.

Equation of line BC is :

`(y-0)/(x+6)=(4-0)/(-2+6) \\\\ y= x +6`

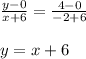
So,the third point that is Locus of point A ,will be no point lying on the line, →y= x +6.

Also, A Triangle is formed, when

Sum of two sides of triangle is greater than third side.

So,third point A will be such that,

1. AB +AC> BC

2. AB +BC> AC

3. AC +BC> AB