Question

What is the quotient of (x^3+3x^2+5x+3)/(x+1)

Answer 1

x² + 2x + 3

Explanation:

given
`(x^3+3x^2+5x+3)/(x+1)`

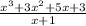
One way of dividing is to use the divisor as a factor in the numerator

Consider the numerator

x²(x + 1) - x² + 3x² + 5x + 3

= x²(x + 1) + 2x(x + 1) - 2x + 5x + 3

= x²(x + 1) + 2x(x + 1) + 3(x + 1) - 3 + 3

= x²(x + 1) + 2x(x + 1) + 3(x + 1) + 0

`(x^3+3x^2+5x+3)/(x+1)`

=
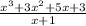
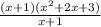`((x+1)(x^2+2x+3))/(x+1)` = x² + 2x + 3 ← quotient