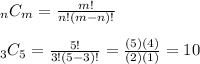Answer:
Step-by-step explanation:
Call the wiiners of the gift cards W₁, W₂, and W₃.
Since each gift card is the same, any permutation of those three winners, W₁, W₂, and W₃ are equivalent. This is what tells that the order of the winners does not matter and that the situation involves a combination instead of a permutation.
Then, you have to calculate the combination of 3 winners, selected from a group of 5 people; that is: