Question

Cobalt 60 has an annual decay rate of 13% how many grams of a 300 g sample one will remain after 20 years round the answer to two decimal places

Answer 1

18.51 grams.

Explanation:

We have been given the decay rate

We have general equation for decay which is:

`y=a\cdot b^t`;
`b=1-r`

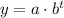Here, we are given with initial sample which is a=300

b=1-13%

And t is 20 years.

We will subatitute the values in the formula we get:

`y=300\cdot (1-(13)/(100))^(20)`

`\Rightarrow y=300((87)/(100))^(20)`

`\Rightarrow y=300(.87)^(20)`

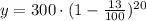
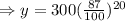
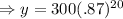
After simplification we get y=18.51 grams.

The sample remain will be 18.51 grams.