Answer:
The length of hypotenuse is
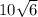 cm
cm
Explanation:
Let's length of hypotenuse is x
Since, a 12 cm altitude to the hypotenuse of a right triangle divides the hypotenuse into segments with ratio 3:2
so,
First part of hypotenuse length is
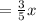
Second part of hypotenuse length is
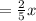
now, we can draw triangle
We can see that
triangles ABD and ABC are similar
so, the ratio of their sides must be equal
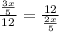
now, we can solve for x
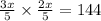
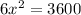
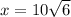
So,
The length of hypotenuse is
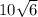 cm
cm