Question

Given: AC and FE bisect each other and Prove: ABCD is a parallelogram.

Answer 1

2)
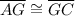`\overline{AG} \cong \overline{GC}` (a segment bisector divides a segment into two congruent segments)

3)
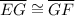`\overline{EG} \cong \overline{GF}` (a segment bisector divides a segment into two congruent segments)

4)
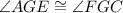`\angle AGE \cong \angle FGC` (vertical angles are congruent)

5)
`\triangle AGE \cong \triangle CGF` (SAS)

6)
`\angle FCG \cong \angle GAE` (CPCTC)

7)
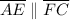`\overline{AE} \parallel \overline{FC}` (converse of alternate interior angles theorem)

8)
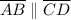`\overline{AB} \parallel \overline{CD}` (segments collinear with parallel segments are parallel)

9)
`\angle DAC \cong \angle ACB` (alternate interior angles theorem)

10)
`\angle DAB \cong \angle DCB` (congruent angles added to congruent angles form congruent angles)

11)
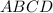`ABCD` is a parallelogram (a quadrilateral with two pairs of opposite congruent angles in a parallelogram)