Question

1.Identify the x- and y-intercepts for y = x2 + 9x + 20.

A.x-int : (–4, 0), (–5, 0); y-int : (0, 20)

B.x-int : (20, 0); y-int : (0,–4), (0, –5)

C.x-int : (0, 20); y-int : (–4, 0), (–5, 0)

D.x-int : (4, 0), (5, 0); y-int : (0, 20)

Answer 1

Hello!

The answer is A.x-int : (–4, 0), (–5, 0); y-int : (0, 20)

Why?

To find the X and Y interceptions of a function, we need to calculate when the function tends to 0.

To identify the X interception we have to make Y equal to 0, so we have the first equation:

`0=X^2+9x+20\\` - This equation is a quadratic equation and it can be easily solved by using the quadratic formula.

Quadratic formula :
`x=(-b ±√(b^2-4*a*c) )/(2*a)`

Where:

- a is equal to the quadratic term coefficient

- b is equal to the lineal term coefficient

- c is equal to the constant number

So, from our quadratic equation we know that:

`a=1\\b=9\\c=20`

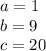
By substituting in the quadratic formula, we have:

`x=(-9 ±√(9^2-4*1*20) )/(2*1)\\`

`x=(-9±√(81-80) )/(2) \\\\x=(-9±1 )/(2)\\\\x1=(-9+1)/(2) =-4\\\\x2=(-9-1)/(2) =-5`

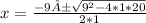
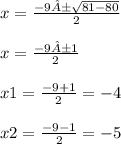
So, we know that x tends to 0 at -4 and -5

X intercepts at (-4,0) and (-5,0)

In order to know when y intercepts, we have to make x equal to 0

Making x equal to 0, we have

`y=0^2+9*0+20\\\\y=20`

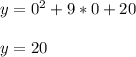
So, now we know that y tends to 0 at 20

Y intercepts once at (0,20)

Have a nice day!

Answer 2

The answer is the option A

`x-int\ (-4, 0), (-5, 0); y-int\ (0, 20)`

Explanation:

we have

`y=x^(2) +9x+20`

we know that

The y-intercept is the value of y when the value of x is equal to zero

The x-intercept is the value of x when the value of y is equal to zero

Using a graphing tool

see the attached figure

The solution is the option A

The x-intercept are
`(-4,0)` and
`(-5,0)`

The y-intercept is the point
`(0,20)`