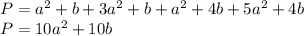Answer:
Area:
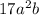
Perimeter:
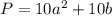
Explanation:
Area
The area of the entire rectangle that is 4b by
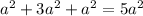 is found using A = l*w. If w=4b and l=
is found using A = l*w. If w=4b and l=
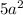 then the area is:
then the area is:
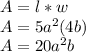
However there is a cutout in the middle. Find the area of the cut out and subtract from the total area.
The cutout is
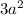 by b. So the area is:
by b. So the area is:

Subtract
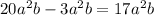
Perimeter
The perimeter is the distance around the entire figure. To find it, add each side length. Then add like terms together.