Question

Saved Suppose that the population of deer in a state is 1,500 and is growing 2% each year. Predict the population after 4 years.

Answer 1

Steps

So for this, we will be creating an equation using the exponential formula - which is
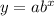`y=ab^x` (a = initial value, b = growth/decay).

Firstly, we know that the original population of the deer is 1,500 so that will be our a value.

Next, we know that the population is growing by 2% annually. With this, we will add 1 and 0.02 (2% in decimal form) since the population is increasing.

• 1 + 0.02 = 1.02

1.02 will be our b variable. Now putting it together, our equation is:
`y=1500(1.02)^x`

Now that we have our equation set up, plug 4 into the x variable and solve for y as such (Remember to not round until the very end):

`y=1500*(1.02)^4\\y\approx 1624`

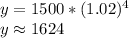
Answer

After 4 years, the deer population will be 1,624.