Answer:
The explanation is given below.
Explanation:
Given for a triangle to be obtuse only one of the angles must be shown to be obtuse but for a triangle to be acute all three angles must be shown to be acute.
According to Pythagoras theorem for a right angled triangle which has one angle of 90° rest of two are acute.
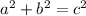
Hence, by Pythagorean inequality
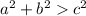
which gives the triangle is acute.
Hence, one acute angle with the Pythagorean inequalities theorem shows that the triangle is acute.