Question

What is the length of the longest side of a triangle that has the vertices (-2, 1), (5, 1), and (5, 4)?

OA. 65 units
OB. √58 units
OC. 6√65 units
OD. 5√65 units

Answer 1

B

Explanation:

To find the length of the longest side of the triangle, first sketch the triangle. A graph paper is not needed here.

In this case we have a right-angled triangle, since the ends of the adjacent side has the same y-coordinate of 1 and the opposite side has the same y-coordinate of 5.

In a right-angled triangle, the hypotenuse side is the longest. The length of the hypotenuse side can be found using 2 methods.

1) Pythagoras' Theorem

a² +b²= c²

(adjacent)² +(opposite)²= (hypotenuse)²

Length of adjacent

= 5 -(-2)

= 7 units

Length of opposite side

= 4 -1

= 3 units

(hypotenuse)²

= 7² +3²

= 58

hypotenuse=
`√(58)`

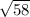
2) Distance formula

Since we know that the hypotenuse side is the longest, we can simply find the length of the hypotenuse side instead of calculating the length of each side.

`\boxed{{\text{Distance between 2 points}= \sqrt{(y_1 - y_2)^(2) + (x_1 - x_2)^(2) } }}`

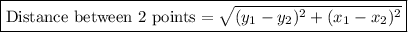
Length of longest side

= distance between (5, 4) and (-2, 1)

`= \sqrt{(4 - 1) {}^(2) + (5 - ( - 2)) {}^(2) }`

`= \sqrt{3 {}^(2) + {7}^(2) }`

`= √(58)`

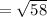
Thus, the length of the longest side is
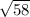`√(58)` units.