Answer:
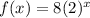
Explanation:
She had 8 subscribers at the beginning of the month. One month later, her number of subscribers doubled and continued to double each month
when month =0 the subscribers = 8 (0,8)
month =1 , subscribers = 16 (1,16)
month = 2, subscribers = 32 and so on (2,32)
Subscribers are doubled every month
For exponential growth we use formula y=ab^x
where 'a' is the initial value. given initial value is 8 so a=8
To frame the function , we plug in (1,16) a=8 and solve for b
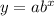
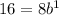
divide by 8 on both sides
b^1 = 2 so b= 2
Exponential function becomes (a=8, b= 2)
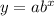
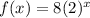
She had 8 subscribers at the beginning of the month
So when month x=0 then the number of subscribers = 8
Domain x starts from 0 month and it goes on increasing
Domain x be the number of months.