Question

The National Science Organization is monitoring the continuous exponential decline of an insect species due to deforestation. They do not know exactly how many there are remaining, but the model they are using represents the minimum number remaining in the world. They are putting measures into place in order to avoid extinction which will take effect when the minimum number reaches a certain point. According to the model, the minimum number of the species remaining, in millions, is constantly decreasing at a rate of 7.9% each year. There are at least 26 million of the species in the world right now. Once the minimum population reaches 2 million, the measures will be instated which should stop the decrease and keep the minimum population at 2 million. If P represents the actual population of the insects in the world, in millions, and t represents the time in years, then which of the following systems of inequalities can be used to determine the possible number of insects in the world over time?

Answer 1

`P\geq 26e^(-0.079t)`

`P\geq 2`

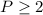
Explanation:

We are given that there is an exponential decay.

Also, the decrease is of constant rate 7.9% i.e. 0.079 each year.

Since, the initial amount of the species is atleast 26 million.

Thus, the inequality for the corresponding model will be,
`P\geq 26e^(-0.079t)`,

where t is the time period for the decay and P is the population.

Moreover, is is given that the population cannot be less than 2 million.

So, we get,
`P\geq 2`.

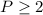Hence, the inequalities to determine the possible number of insects over time are given by,

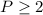`P\geq 26e^(-0.079t)`

`P\geq 2`.