Question

What is the value of m in the figure below in this diagram abd bcd

Answer 1

`\triangle BCA\ \text{and}\ \triangle DCB\ \text{are similar (AAA). Therefore the sides are in proportion:}\\\\(BC)/(CD)=(AC)/(BC)\\\\\text{We have}\\\\BC=m\\CD=7\\AC=7+11=18\\\\\text{Substitute:}\\\\(m)/(7)=(18)/(m)\qquad\text{cross multiply}\\\\m^2=(7)(18)\\\\m^2=126\to\boxed{m=√(126)}\to\boxed{A.}`

Answer 2

The value of m in the figure is
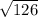`√(126)`. Hence the correct option is a.

In the given diagram where AABD~ is presented, indicating that triangles AABD and ADB are similar right triangles, the value of m can be determined through the ratio of corresponding sides. In similar right triangles, the ratios of corresponding sides are constant. The side opposite the right angle in triangle AABD corresponds to side AD in triangle ADB.

Let x represent the common ratio. Therefore, the proportion is set up as follows: AB/BD = AD/AB. Since AB=m, the equation becomes BD/m = AD/m.

Given that AD=11, we can substitute this value into the equation and solve for m: m/BD = 11/m

Cross-multiplying gives m^2=11×BD. To find m, we need the value of BD.

Looking at the answer choices, the only one that satisfies m^2 =11×BD is

m=126. Therefore, m is determined to be
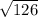`√(126)` in this context. Hence the correct option is a.