Question

A line parallel to a triangle’s side splits one side into lengths of 9 and 3. The other side is split into lengths of 12 and x. What is the value of x? (Enter the number only)

Answer 1

The value of x = 4.

Explanation:

As per figure attached line DE is parallel to BC.

DE splits line AB into lengths 9 and 3.Similarly splits the other side AC of the triangle into 12 and x.

Now we can see that ΔABC and ΔADE are similar because they follow the rule all angles of ΔABC are same of ΔADE.

Therefore
`(AD)/(AB)=(AE)/(AC)`

⇒
`(9)/(12)=(12)/((12+x))`

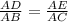
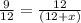
Now we cross multiply the fractions of both the sides.

9(x+12) = 12×12

9x+108 = 144

9x+108-108 = 144-108

9x = 36

`x= (36)/(9)`

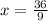
x = 4.