Question

The hypotenuse of a right triangle has length 13 units, and one leg has length 12 units. How long is the other leg?

17.7 units


-17.7 units


5 units


-5 units

Answer 1

Using Pythagorean Theorem, we get:

`x=√(13^2-12^2)=5`

Answer 2

5 units is the length of the other leg.

Explanation:

A right triangle consists of two legs and a hypotenuse. The two legs meet at a 90° angle and the hypotenuse is the longest side of the right triangle and is the side opposite the right angle.

If we know the lengths of two sides of a right angled triangle, we can find the length of the third side with the help of the Pythagorean Theorem.

The Pythagorean Theorem

If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse.

This relationship is represented by the formula:

`a^2+b^2=c^2`

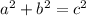
We know that the hypotenuse of a right triangle has length 13 units, and one leg has length 12 units.

Using the above formula we can find the length of the other leg as follows:

`12^2+b^2=13^2`

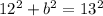
Solving for b

`12^2+b^2-12^2=13^2-12^2\\b^2=25\\b=√(25)\\b=5`

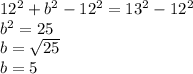
5 units is the length of the other leg.