Question

Expand and combine like terms. (5a^3 - 2)(5a^3+2)

Answer 1

The multiplication can be transformed into the difference of squares using the rule:(a−b)(a+b)=a²-b² . Gets the square of 2.

(5a³)²-4

Expand (5a³)².

5² (a³)² -4

To raise a power to another power, multiply the exponents. Multiply 3 and 2 to get 6.

5²a⁶-4

25a⁶-4 ====> Answer

{ Pisces04 }

Answer 2

`25a^6-4`

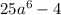
Explanation:

So if you look at the equation, you'll notice it's being multiplied by it's conjugate which can be expressed as: x+a and x-a. See how only the sign changes? Well if remember the differences of squares, it looks like that, because it is. Essentially the difference of squares says that:
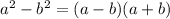`a^2-b^2=(a-b)(a+b)`. So expanding this out will result in
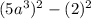`(5a^3)^2-(2)^2` which simplifies to:
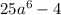`25a^6-4`. If you're confused on how I got 25a^6. Try to think of a^3 as three a's rather than simply an exponent. and since it has a coefficient of 5. 5a^3 is the same as (5 * a * a * a). Now if you square this you have (5 * a * a * a) * (5 * a * a * a). So if you group like terms you'll end up with 6 a's being multiplied by each other (which can be expressed as a^6) and 5 * 5 which is 25.