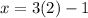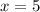Question

In parallelogram DEFG, DH = x + 1, HF = 3y,

GH=3x−4,and HE = 5y + 1. Find the values of x and y. The diagram is not drawn to scale

Answer 1

ANSWER


`x = 5 \: and \: = 2`

Step-by-step explanation


The diagonals of a parallelogram bisects each other.

Therefore


`DH=HF`


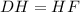
This implies that,


`x + 1 = 3y`

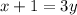
We make x the subject to get,


`x = 3y - 1...eqn1`

Similarly,



`GH=HE`


`3x - 4 = 5y + 1`


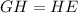
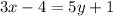
This implies that,


`3x - 5y = 5...eqn2`


We substitute equation (1) in to equation (2) to get,


`3(3y - 1) - 5y = 5`


We expand the bracket to get,


`9y - 3 - 5y = 5`


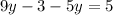
We group like terms to get,



`9y - 5y = 5 + 3`



`4y = 8`

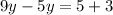
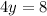
Divide both sides by 4 to obtain,


`y = 2`


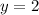
We put the value of y into equation (3) to get,



`x = 3(2) - 1`



`x = 5`