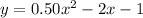Question

Can someone please help me

Answer 1

Vertex form:
`y=(1)/(2)(x-2)^2-3`

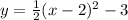
Standard Form:
`y=0.50x^2-2x-1`

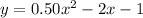
Explanation:

Well the vertex form of an equation is given in the form:
`y=a(x-h)^2+k` where (h, k) is the vertex, and by looking at the graph, you'll see the vertex is at (2, -3). So plugging this into the equation gives you:
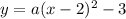`y=a(x-2)^2-3`. Now to find a which will determine the stretch/compression, you can substitute any point in (besides the vertex, because that'll result in (x-2) being 0). So I'll use the point (0, -1) which is the only point I think I can accurately determine by looking at the graph (besides (4, -1) since it's symmetric). Anyways I'll plug this in

Plug in (0, -1) as (x, y)

`-1 = a(0-2)^2-3`

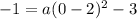
calculate inside the parenthesis

`-1 = a(-2)^2-3`

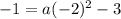
square the -2

`-1 = 4a-3`

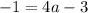
Add 3 to both 3 to both sides

`2 = 4a`

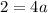
divide both sides by 4

`a=(1)/(2)`

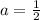
This gives you the equation:
`y=(1)/(2)(x-2)^2-3`

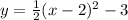
To convert this into standard form you simply expand the square binomial, you can use the foil method to achieve this, but it generally expands to:
`(a+b)^2=a^2+2ab+b^2`.

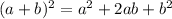Original equation:

`y=(1)/(2)(x-2)^2-3`

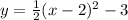
expand square binomial:

`y=(1)/(2)(x^2-4x+4)^2-3`

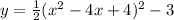
Distribute the 1/2

`y=0.50x^2-2x+2-3`

Combine like terms:

`y=0.50x^2-2x-1`