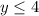Answer:
Explanation:
we know that
The equation of a vertical parabola into vertex form is equal to
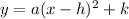
where
(h,k) is the vertex of the parabola
if a>0 -----> the parabola open upward (vertex is a minimum)
if a<0 -----> the parabola open downward (vertex is a maximum)
Verify each case
case A)

The vertex is the point
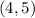

a>0 -----> the parabola open upward (vertex is a minimum)
The range is the interval--------> [5,∞)
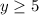
case B)
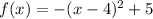
The vertex is the point
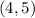

a<0 -----> the parabola open downward (vertex is a maximum)
The range is the interval--------> (-∞,5]
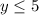
case C)
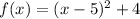
The vertex is the point


a>0 -----> the parabola open upward (vertex is a minimum)
The range is the interval--------> [4,∞)
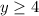
case D)
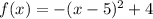
The vertex is the point


a<0 -----> the parabola open downward (vertex is a maximum)
The range is the interval--------> (-∞,4]