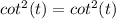Question

Verify csc^2t-cos t sect= cot^2 t

Answer 1

Rewriting the left hand side,

csc²t - cost sec t

= (1/sin²t)-(cost)(1/cost)

= 1/sin²t - 1

= 1/sin²t - sin²t/sin²t

= (1-sin²t)/sin²t

= cos²t/sin²t

= cot²t

Answer 2

Explanation:

assuming this is correct, you can really manipulate either side and you should arrive eventually arrive to same sides. But in this case you usually manipulate the more complex side. So I'll manipulate the left side.

Original Equation:

`csc^2(t)-cos(t)*sec(t)=cot^2(t)`

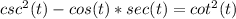
Rewrite csc and sec, using the reciprocal identities:

`((1)/(sin(t)))^2-cos(t)*(1)/(cos(t))=cot^2(t)`

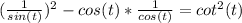
multiply cos(t) and 1/cos(t) and also distribute the exponent:

`(1)/(sin^2t)-1=cot(t)^2`

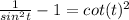
Multiply 1 by sin^2(t)/sin^2(t)

`(1)/(sin^2(t))-(sin^2(t))/(sin^2(t))`

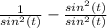
subtract the numerator

`(1-sin^2(t))/(sin^2(t))`

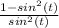
Pythagorean Identity:

`sin^2(t)+cos^2(t)=1`

subtract sin^2(t) from both sides

`cos^2(t)=1-sin^2(t)`

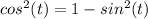
Use this to rewrite the numerator:

`(cos^2(t))/(sin^2(t))`

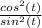
Rewrite using the reciprocal identities:

`cot^2(t) = cot^2(t)`