Question

Find the zeros of each function. State the multiplicity of any multiple zeros. (Please show work)

16. Y=3x(x+2)^3
17. Y=x^4-8x^2+16

Answer 1

QUESTION 16

The given function is,


`y = 3x {(x + 2)}^(3)`

To find the zeroes of this function, we equate the function to zero to get,


`3x {(x + 2)}^(3) = 0`

We now apply the zero product principle to get,


`3x = 0 \: or \: {(x + 2)}^(3) = 0`

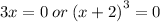
The second factor is repeating 3 times, therefore the root has a multiplicity of 3.

This implies that,


`x = 0 \: or \: x = - 2`
-2 has a multiplicity of 3.

QUESTION 17.

The given expression is


`{x}^(4) - 8 {x}^(2) + 16 = 0`


`({x}^(2)) ^(2) - 8 {x}^(2) + 16 = 0`

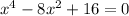
This is now a quadratic equation in x².

We split the middle term to get,


`({x}^(2)) ^(2) - 4 {x}^(2) - 4 {x}^(2) + 16 = 0`

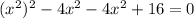
We now factor to obtain,


`{x}^(2) ( {x}^(2) - 4) - 4( {x}^(2) - 4) = 0`

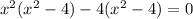
This implies that,


`( {x}^(2) - 4)( {x}^(2) - 4) = 0`


`( {x}^(2) - 2^2)( {x}^(2) - 2^2) = 0`

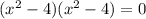
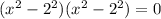
We apply difference of two squares here to get,


`(x - 2)(x + 2)(x - 2)(x + 2) = 0`

This is the same as,


`(x - 2) ^(2) (x + 2) ^(2) = 0`

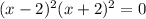
This time both roots have a multiplicity of 2.

Applying the zero product property, we obtain,


`(x - 2) ^(2) = 0 \: or \: (x + 2) ^(2) = 0`

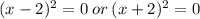
This implies that,


`x = 2 \: or \: - 2`

with a multiplicity of 2 each.