Question

PLEASE HELP ME.

Determine which consecutive integers have a real zero of the function f(x)=x^4-3x^3-2x^2+3x-5. between them.

a.(-6, -5), (3, 4)
b.(-2, -1), (3, 4)
c.(-6, -5), (-2, -1)
d. (1, 2), (-4, -3)

Answer 1

b.(-2, -1), (3, 4)

Explanation:

We are given function as

`f(x)=x^4-3x^3-2x^2+3x-5`

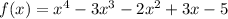
We can verify each intervals

At (-6,-5):

Firstly we will plug x=-6

`f(-6)=(-6)^4-3(-6)^3-2(-6)^2+3(-6)-5=1849`

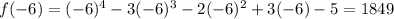
now, we can plug x=-5

`f(-5)=(-5)^4-3(-5)^3-2(-5)^2+3(-5)-5=930`

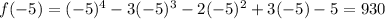
since, both are positive values

So, zeros can not lie between them

At (-4,-3):

Firstly we will plug x=-4

`f(-4)=(-4)^4-3(-4)^3-2(-4)^2+3(-4)-5=399`

now, we can plug x=-3

`f(-3)=(-3)^4-3(-3)^3-2(-3)^2+3(-3)-5=130`

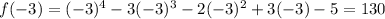
since, both are positive values

So, zeros can not lie between them

At (-2,-1):

Firstly we will plug x=-2

`f(-2)=(-2)^4-3(-2)^3-2(-2)^2+3(-2)-5=21`

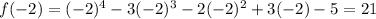
now, we can plug x=-1

`f(-1)=(-1)^4-3(-1)^3-2(-1)^2+3(-1)-5=-6`

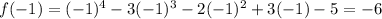
since, one is positive and another is negative

So, zeros will lie between them

At (3,4):

Firstly we will plug x=3

`f(3)=(3)^4-3(3)^3-2(3)^2+3(3)-5=-14`

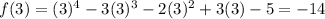
now, we can plug x=4

`f(4)=(4)^4-3(4)^3-2(4)^2+3(4)-5=39`

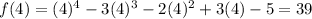
since, one is positive and another is negative

So, zeros will lie between them

zeros will be between

(-2, -1), (3, 4)