Answer:
The measure of angle YUV is equal to
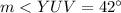
Explanation:
see the attached figure to better understand the problem
we have that
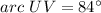 -----> given problem
-----> given problem
so
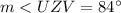 ------> by central angle
------> by central angle
we know that
The triangle UZV is an isosceles triangle
because
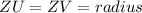
so
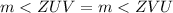 -----> bases angle of the isosceles triangle
-----> bases angle of the isosceles triangle
Remember that
The sum of the internal angles of a triangle is equal to
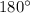
so
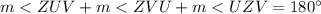
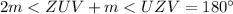
substitute and solve for m<ZUV
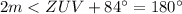
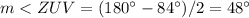
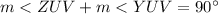 ------> by complementary angles
------> by complementary angles
solve for m<YUZ

