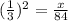Question

A right cylinder has a radius of 6 m and a surface area of 84 m². Find the surface area of a similar cylinder with a radius of 2 m.

Answer 1

The surface area of the second cylinder is equal to
`9.33\ m^(2)`

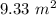
Explanation:

we know that

If two figures are similar then

the ratio of their surfaces areas is equal to the scale factor squared

Let

z-------> the scale factor

x------> the surface area of the smaller cylinder (second cylinder)

y-------> the surface area of the original cylinder (first cylinder)

so

`z^(2)=(x)/(y)`

Step 1

Find the scale factor

`z=(2)/(6)=(1)/(3)`

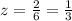
Step 2

Find the surface area of the second cylinder

we have

`z=(1)/(3)`

`y=84\ m^(2)`

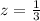
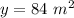
substitute and solve for x

`((1)/(3))^(2)=(x)/(84)`

`x=(1)/(9)*84=9.33\ m^(2)`