Question

What are the approximate values of the minimum and maximum points of f(x) = x5 − 10x3 + 9x on [-3,3]? A. maximum point: (–2.4, 37.014) and minimum point: (2.4, –37.014) B. maximum point: (2.4, –37.014) and minimum point: (–2.4, 37.014) C. maximum point: (–1.4, 33.014) and minimum point: (1.4, –33.014) D. maximum point: (–3, 30) and minimum point: (3, –30)

Answer 1

(-2.4, 37.014)

Explanation:

We are not told how to approach this problem.

One way would be to graph f(x) = x^5 − 10x^3 + 9x on [-3,3] and then to estimate the max and min of this function on this interval visually. A good graph done on a graphing calculator would be sufficient info for this estimation. My graph, on my TI83 calculator, shows that the relative minimum value of f(x) on this interval is between x=2 and x=3 and is approx. -37; the relative maximum value is between x= -3 and x = -2 and is approx. +37.

Thus, we choose Answer A as closest approx. values of the min and max points on [-3,3]. In Answer A, the max is at (-2.4, 37.014) and the min at (2.4, -37.014.

Optional: Another approach would be to use calculus: we'd differentiate f(x) = x^5 − 10x^3 + 9x, set the resulting derivative = to 0 and solve the resulting equation for x. There would be four x-values, which we'd call "critical values."

Answer 2

A. Maximum point :(-2.4,37.014)

Minimum point: (2.4,-37.014).

Explanation:

Given function

f(x)=
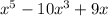`x^5-10x^3+9x` on interval
`\left[ -3, 3\right]`

A. Maximum point (-2.4,37.014)

Minimum point (2.4,-37.014)

f(x)=
`(-2.4)^5-10(-2.4)^3+9(-2.4)`

f(x)=-79.62624+138.24-21.6

f(x)=37.014

Put x= 2.4 then we get

f(x)=
`(2.4)^5-10(2.4)^3+9(2.4)`

f(x)=79.62624-138.24+21.6

f(x)=37.014

B. Maximum point (2.4,-37.014)

Minimum point (-2.4,37.014)

Put x= 2.4. Then we get

f(x)= -37.014

Put x=-2.4 then we get

f(x)= 37.014

C. Maximum point ( -1.4, 33.014)

Minimum point ( 1.4, -33.014)

Put x=-1.4 then we get

f(x)=
`(-1.4)^5-10(-1.4)^3+9(1.4)`

f(x)=-38.94

Put x= 1.4 then we get

f(x)= 38.94

D. Maximum point ( -3,30)

Minimum point ( 3,-30)

Put x=3 then we get

f(x)= 243-270+27=0

Put x=-3 then we get

f(x)= -243+270-27=0

Hence , from option A,B,C and D we can see only option A is right answer.

The approximate values of the minimum point (2.4,-37.014) and maximum point (-2.4, 37.014) of the function f(x)=
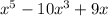`x^5-10x^3+9x` on
`\left[-3,3\right]`.