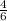Question

The ratio of the numerator to the denominator of a fraction is 2 to 3. If both the numerator and the denominator are increased by 2, the fraction becomes 3/4 . What is the original fraction? Which of the following systems of equations can be used to solve the problem?

A. n + 4 = 3 and d + 5 = 4
B. 3n - 2d = 0 and 4n + 2 = 3d + 2
C. 3n = 2d and 4n + 8 = 3d + 6

Answer 1

The fraction is
`(4)/(6)`

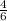
Option (B) is correct.

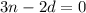`3n-2d=0` and
`4n+8=3d+6`

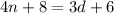
Explanation:

Let n denotes numerator and d denotes denominator of the fraction.

Given : The ratio of the numerator to the denominator of a fraction is 2 to 3.

That is
`(n)/(d)=(2)/(3)`

Cross multiply , we get,

`3n=2d`

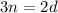
Or,
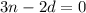`3n-2d=0` ........(1)

Also, given : . If both the numerator and the denominator are increased by 2, the fraction becomes 3/4

That is
`(n+2)/(d+2)=(3)/(4)`

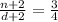
Cross multiply , We get,

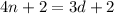
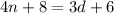`4{n+2}={3}{d+2}`

`4n+8=3d+6` .........(2)

`3d-4n=2` .......(3)

Thus, from (1) and (2) , option (B) follows.

Solving equation (1) and (3) to get the original fraction using elimination method,

3n - 2d = 0 ............(1)

and 3d - 4n = 2 .........(3)

Multiply equation (1) by 3 , we get ,

9n - 6d = 0 ..........(4)

Multiply equation (3) by 2 , we get ,

-8n + 6d = 4 ..........(5)

Adding (4) and (5) , we get,

9n - 6d -8n + 6d = 4 + 0

⇒ n = 4

Put n = 4 in (1), we get

3n - 2d = 0 ⇒ 3(4) - 2d = 0 ⇒ 12 -2d = 0 ⇒ 12 = 2d ⇒ d = 6

so, the numerator is 4 and the denominator is 6.

Thus, the fraction is
`(4)/(6)`