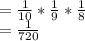Answer:
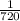
Explanation:
If we arrange the first three cars one by one we get -
Selecting the first car out of ten cars
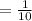
Selecting the second car out of remaining nine cars
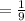
Selecting the third car out of remaining eight cars
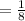
So, the probability of selecting three cars back to back without repeating is given by
Probability of Selecting the first car out of ten cars * Probability of Selecting the second car out of remaining nine cars * Probability of Selecting the third car out of remaining eight cars