Answer:
a)
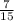
b) There are 30 balls
c) Number of blue balls added = 10, number of red balls added = 0 and number of yellow balls added = 0
Explanation:
a) Sub of the probabilities is always 1.
Therefore,
p(red) + p(blue) + p(yellow) = 1
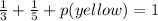
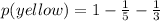
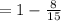
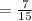
b) p(red ball) =
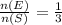
But, it is given that n(E) = 10
Therefore,
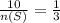
n(S) = 30
Hence, there are 30 balls in total
c) From b), there are 10 red balls.
Now, p(blue ball) =
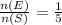
Since, n(S) = 30,
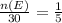
n(E) = 6
There are 6 blue balls and
the number of yellow balls = 30 - (10 + 6) = 14
After adding 10 balls, n(S) = 40
p(blue ball) =

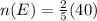
= 16
But, number of blue balls before addition = 6.
Hence, all the added balls are blue.