Question

A hair salon is offering haircuts at discounted prices. Each cut for short hair costs $20, and each cut for long hair costs $35. The first day the salon used the discounted prices, the hairdressers earned a total of $1,070 from haircuts. The hairdressers gave a total of 37 haircuts that day. Answer the questions that follow to write a system of linear equations that models this situation.

1) Let x represent the number of haircuts for short hair. Let y represent the number of haircuts for long hair.

A haircut for short hair costs $20, and a haircut for long hair costs $35. The salon earned a total of $1,070 from haircuts the first day. Write an equation in standard form that models the salon’s earnings from each type of haircut that day.

2) Let x represent the number of short haircuts. Let y represent the number of long haircuts.

The salon gave a total of 37 haircuts for short and long hair the first day. Write an equation in standard form that models the number of short and long haircuts given that day.

Answer 1

X=20

Y=35

1070=35Y+20X

X+Y=37

Answer 2

`20x+35y=1070`

`x+y=37`

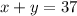
Explanation:

Each cut for short hair costs $20, and each cut for long hair costs $35.

Let x represent the number of haircuts for short hair.

Let y represent the number of haircuts for long hair.

Part 1:

`20x+35y=1070` .....(1)

Part 2:

The salon gave a total of 37 haircuts for short and long hair the first day.

`x+y=37`

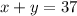
Further if you want to solve it:

Substituting
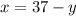`x=37-y` in equation (1)

`20(37-y)+35y=1070`

`740-20y+35y=1070`

`15y=330`

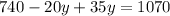
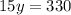
y = 22

And x = 37-y

`x=37-22=15`

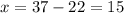
x = 15

Hence, there were 15 haircuts for short hair and 22 haircuts for long hair.