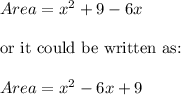Question

Which polynomial expression represents the area of the outermost square tile, shown below?

A square shaped tile with length x minus three is shown


x2 + 6x − 6

x2 − 9x + 6

x2 + 6x − 9

x2 − 6x + 9

Answer 1

The polynomial expression represents the area of the outermost square tile, is:

`x^2-6x+9`

Explanation:

We are asked to find the area of a square side whose length of side is given to be:

Side length(s)=
`x-3`

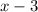
The area of a square of side length " s " is given by:

`Area=s^2`

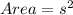
Hence, the area of square tile is calculated by:

`Area=(x-3)^2`

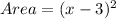
Now, we know that:

`(a-b)^2=a^2+b^2-2ab`

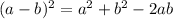
on expanding the term of the area we get:

`Area=x^2+9-6x\\\\\text{or\ it\ could\ be\ written\ as:}\\\\Area=x^2-6x+9`

Answer 2

I believe the last choice is your answer. See when dealing with polynomials, you need to factor. A polynomial can be broken down into this:
A+B+C or a variation of it.
that is simplifying the polynomial. This is done by finding two numbers that add up to the b term and multiply to the c term.
Let’s start with the first option. The first option is unfactorable as there are no two numbers that add to six and multiply to six.
The same applies for the second option. C is also unfactorable. Leaving D as your final option. When factored, it will give you (x-3)(x-3) or (x-3)^2. Note that this is a difference of squares, meaning that it has a formula: (a-b)^2= a^2-2AB+B^2. Meaning, (x-3)2 is equal to x2-2(3x)+3^2= x2-6x+9. Hope this helped.