Question

Two particles are fixed to an x axis: particle 1 of charge −1.50 ✕ 10−7 c at x = 6.00 cm, and particle 2 of charge +1.50 ✕ 10−7 c at x = 27.0 cm. midway between the particles, what is their net electric field? (express your answer in vector form.) e = −244897.96i correct: your answer is correct. n/c

Answer 1

Answer :
`\underset{E_(R)}{\rightarrow} =-2.44*10^(5)\ \widehat{i} \ (N)/(C)`

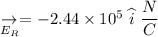
Explanation :

Given that,

Charge of particle 1 =
`-1.50*10^(-7) c`

Distance x = 6 cm

Charge of particle 2 =
`1.50*10^(-7) c`

Distance x = 27 cm

Total distance =
`(6+27)/(2)`

`r = 16.5\ cm`

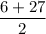
Particle 1 is at (6,0) and particle 2 is at (27,0) .

Therefore, midway (16.5, 0)

Now,
`r = (|6-16.5|)/(2) = (|27-16.5|)/(2) = 10.5\ cm`

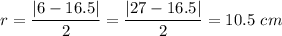
Formula of electric field

`E = (1)/(4\pi\epsilon_(0))*(q)/(r^(2))`

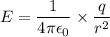
Now, the the electric field due to particle 1

`\underset{E}{\rightarrow}\ = -(9*10^(9)*1.50*10^(-7 ))/(10.5)\ \widehat{i}  (N)/(C)`

`\underset{E}{\rightarrow} = (13.5*10^(2))/((10.5*10^(-2))^(2))\widehat{i}  (N)/(C)`

`\underset{E}{\rightarrow} = -1.22*10^(5)\ \widehat{i} \ (N)/(C)`

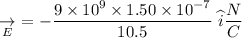
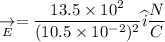
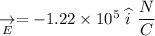
Similarly, the electric field due to particle 2

`\underset{E}{\rightarrow} = -1.22*10^(5)\ \widehat{i} \ (N)/(C)`

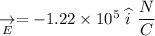
Resultant Electric field

`\underset{E_(R)}{\rightarrow} = \underset{E_(1)}{\rightarrow} + \underset{E_(2)}{\rightarrow}`

`\underset{E_(R)}{\rightarrow} = -2.44*10^(5)\ \widehat{i} \ (N)/(C)`

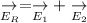
Hence, this is the required answer.