Answer:
27,400 is the current population
7% is the rate of increase
The new size is:
- 38,430 is the population if t is an exponent
- 146,590 is t is NOT an exponent in the formula you typed
Explanation:
To find the population in a future year, use the formula:
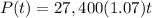
Substitute the value t=5 to find the population in 5 years.
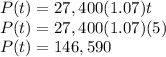
Or if the equation is supposed to have t as an exponent then look below:

Substitute the value t=5 to find the population in 5 years.

This formula is based off the standard formula
 so r, the rate is 1.07=1+0.07 so r is 7%.
so r, the rate is 1.07=1+0.07 so r is 7%.
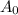 is the starting population which is 27,400 here.
is the starting population which is 27,400 here.