Question

1.Afla numarul abc,stiind ca abc:15=16 rest 1

\

2.Gaseste numarul necunoscut:a 486:x=17 b y:18=35 rest 1 c 730:z=27 rest 1




3.Diferenta a doua numere naturale este70.Impartind numarul mai mare la numarul mic,obtinem catul 8 si restul.Care sunt numerele?





ajutatima va rooog!

Answer 1

Explanation:

Ques 1)

abc: 15 = 16 rest 1

that means that if abc is divided by 15 than we get the quotient as 16 and remainder as 1.

Hence using : dividend=divisor×quotient+remainder we have:

abc=15×16+1

Hence, the value of abc is 241.

Ques 2)

a)

486: x = 17

i.e.
`(486)/(x)=17`

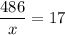
⇒ x=486×17=8262

b)

y: 18 = 35 rest 1

that means when y is divided by 18 we get the quotient as 35 and remainder as 1.

Hence using : dividend=divisor×quotient+remainder we have:

y=35×18+1=631

y=631

c)

730: z = 27 rest 1

that means when 730 is divided by z we get the quotient as 27 and remainder as 1.

Hence using : dividend=divisor×quotient+remainder we have:

730=27z+1

27z=730-1

27z=729

z=27 (dividing both side by 27)

Ques 3)

Let'a' and 'b' denote the two natural numbers such that a is greater than 'b'.

a-b=70----(1)

also when a is divided by b then we get the quotient as 8 and some remainder.

Let the remainder be 'r'.

this means a=8b+r

let us consider r=0.

a=8b

hence from (1) we have

7b=70

b=10 (on dividing both side by 7)

hence a=80.

when r=1,2,3,4,5,6

we do not get a natural number as value for a and b.

also when r=7 we get the value of b=9 and a=79

After r>7 we get the value of b<r such a condition is not possible.