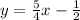Question

An equation parallel and perpendicular to 4x+5y=19

Answer 1

Parallel line:

`y=-(4)/(5)x+(9)/(5)`

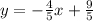
Perpendicular line:

`y=(5)/(4)x-(1)/(2)`

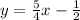
Explanation:

we are given equation 4x+5y=19

Firstly, we will solve for y

`4x+5y=19`

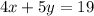
we can change it into y=mx+b form

`5y=-4x+19`

`y=-(4)/(5)x+(19)/(5)`

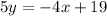
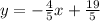
so,

`m=-(4)/(5)`

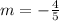
Parallel line:

we know that slope of two parallel lines are always same

so,

`m'=-(4)/(5)`

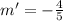
Let's assume parallel line passes through (1,1)

now, we can find equation of line

`y-y_1=m'(x-x_1)`

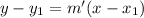
we can plug values

`y-1=-(4)/(5)(x-1)`

now, we can solve for y

`y=-(4)/(5)x+(9)/(5)`

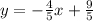
Perpendicular line:

we know that slope of perpendicular line is -1/m

so, we get slope as

`m'=(5)/(4)`

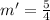
Let's assume perpendicular line passes through (2,2)

now, we can find equation of line

`y-y_1=m'(x-x_1)`

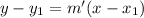
we can plug values

`y-2=(5)/(4)(x-2)`

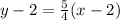
now, we can solve for y

`y=(5)/(4)x-(1)/(2)`