Question

The angle of elevation from the bottom of a scenic gondola ride to the top of a mountain is 26. If the vertical distance from the bottom to the top of the mountain is 725 feet, what is the length of the gondola ride? round to the nearest foot.

A. 625 ft
b. 1654 ft
c. 807 ft
d. 318 ft
need asap please help

Answer 1

1654 feet

Explanation:

Answer 2

The length of gondola ride is 1654 feet.

Explanation:

Given,

Angle of elevation from bottom of a scenic gondola ride to the top of mountain = 26

Vertical distance from the bottom to top of mountain = 725 feet

We need to find length of gondola ride.

By using trigonometric relation,

SinΘ =
`(Perpendicular)/(Hypotenuse)`

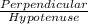
Here, Perpendicular is the vertical distance and is equal to 725 feet

Θ is the angle of elevation and is equal to 26

And hypotenuse is the length of gondola ride.

So,

Sin26 =
`(725)/(Hypotenuse)`

Hypotenuse =
`(725)/(sin26)`

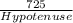
Hypotenuse = 1653.84 ≈ 1654 feet

Hence, the length of gondola ride is 1654 feet.