Answer:
Only option A is correct.
Explanation:
From the given figure it is noticed that the vertices of hyperbola are (0,8) and (0,-8). It is a vertical hyperbola.
It means a=8.
From the rectangle we can say that the value of b is 6.
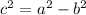
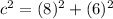
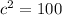

The focus of a vertical hyperbola are (0,c) and (0,-c). So, the focus of hyperbola are (0,10) and (0,-10).
Therefore option A is correct.
Asymptotes of a vertical hyperbola are
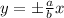
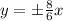
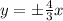
Directrix of a vertical hyperbola are
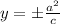
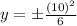
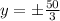
Only option A is correct.