Answer:
Factored form:
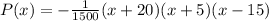 .
.
Standard form:

Explanation:
The factor form of a polynomial is
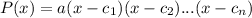
where, a is a constant and leading coefficient,
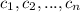 are n zeroes of the polynomial.
are n zeroes of the polynomial.
From the given graph it is clear that the x-intercepts of the function are -20, -5 and 15. It means the zeroes of the given function are -20, -5 and 15. So, the required function is
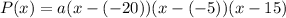
 .... (1)
.... (1)
From the given graph it is clear that y-intercept of the function is (0,1). Use the y-intercept of the graph to find the value of a.
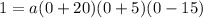
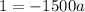
Divide both sides by -1500.

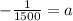
Put
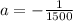 in equation (1).
in equation (1).
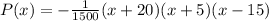
Therefore the factored form of the function is
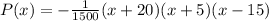 .
.
Expand the above function to find the standard form of the function
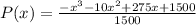

Therefore the standard form of the function is
 .
.