Question

If −6x+y=−4 and −8x−10y=3 are true equations, what would be the value of 2x+11y?

Answer 1

Answer: -7

=========================================================

Reason:

The equation −8x−10y=3 is the same as 8x+10y = -3 after multiplying both sides by -1

We have this system of equations

`\begin{cases}-6x+y = -4\\8x+10y = -3\end{cases}`

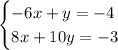
Add the equations straight down.

• -6x+8x becomes 2x
• y+10y becomes 11y
• the right hand sides combine to -4+(-3) = -7

Therefore, we end up with the equation 2x+11y = -7

An alternative is to solve the system using substitution to get the (x,y) intersection point. Then use those coordinates to compute 2x+11y and you should get -7 as a result.