Answer:
Length is 20 in
Height is 4 in
Explanation:
we are given
The width of a rectangular box is 8in
so,
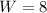
The height is one fifth the length
Let's assume length =x
L=x

now, we can find volume

we can plug
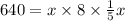
now, we can solve for x

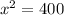

so, L=20 in
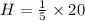
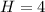
So,
Length is 20 in
Height is 4 in