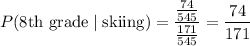10.

155 of the total 545 students belong to the 6th grade. 46 of the total 545 students belong to the 6th grade and like ice skating. In terms of probability,
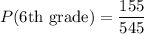
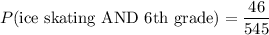
So

11. Similar setup. We know 171 of 545 students like skiing, and there are 74 8th graders that like skiing. So